Accurate computational prediction of chemical processes from the quantum mechanical laws that govern them is a tool that can unlock new frontiers in chemistry, improving a wide variety of industries. Unfortunately, the exact solution of quantum chemical equations for all but the smallest systems remains out of reach for modern classical computers, due to the exponential scaling in the number and statistics of quantum variables. However, by using a quantum computer, which by its very nature takes advantage of unique quantum mechanical properties to handle calculations intractable to its classical counterpart, simulations of complex chemical processes can be achieved. While today’s quantum computers are powerful enough for a clear computational advantage at some tasks, it is an open question whether such devices can be used to accelerate our current quantum chemistry simulation techniques.
In “Hartree-Fock on a Superconducting Qubit Quantum Computer”, appearing today in Science, the Google AI Quantum team explores this complex question by performing the largest chemical simulation performed on a quantum computer to date. In our experiment, we used a noise-robust variational quantum eigensolver (VQE) to directly simulate a chemical mechanism via a quantum algorithm. Though the calculation focused on the Hartree-Fock approximation of a real chemical system, it was twice as large as previous chemistry calculations on a quantum computer, and contained ten times as many quantum gate operations. Importantly, we validate that algorithms being developed for currently available quantum computers can achieve the precision required for experimental predictions, revealing pathways towards realistic simulations of quantum chemical systems. Furthermore, we have released the code for the experiment, which uses OpenFermion, our open source repository for quantum computations of chemistry.
Developing an Error Robust Quantum Algorithm for Chemistry
There are a number of ways to use a quantum computer to simulate the ground state energy of a molecular system. In this work we focused on a quantum algorithm “building block”, or circuit primitive, and perfect its performance through a VQE (more on that later). In the classical setting this circuit primitive is equivalent to the Hartree-Fock model and is an important circuit component of an algorithm we previously developed for optimal chemistry simulations. This allows us to focus on scaling up without incurring exponential simulation costs to validate our device. Therefore, robust error mitigation on this component is crucial for accurate simulations when scaling to the “beyond classical” regime.
Errors in quantum computation emerge from interactions of the quantum circuitry with the environment, causing erroneous logic operations – even minor temperature fluctuations can cause qubit errors. Algorithms for simulating chemistry on near-term quantum devices must account for these errors with low overhead, both in terms of the number of qubits or additional quantum resources, such as implementing a quantum error correcting code. The most popular method to account for errors (and why we used it for our experiment) is to use a VQE. For our experiment, we selected the VQE we developed a few years ago, which treats the quantum processor like an neural network and attempts to optimize a quantum circuit’s parameters to account for noisy quantum logic by minimizing a cost function. Just like how classical neural networks can tolerate imperfections in data by optimization, a VQE dynamically adjusts quantum circuit parameters to account for errors that occur during the quantum computation.
Enabling High Accuracy with Sycamore
The experiment was run on the Sycamore processor that was recently used to demonstrate quantum supremacy. Though our experiment required fewer qubits, even higher quantum gate fidelity was needed to resolve chemical bonding. This led to the development of new, targeted calibration techniques that optimally amplify errors so they can be diagnosed and corrected.
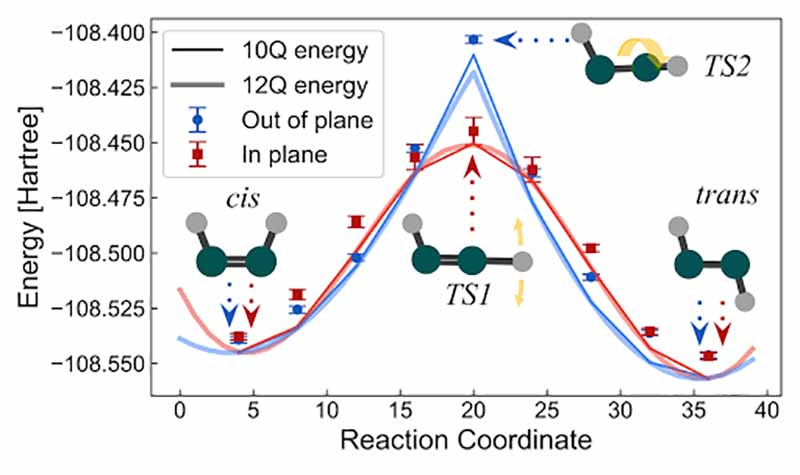
Energy predictions of molecular geometries by the Hartree-Fock model simulated on 10 qubits of the Sycamore processor.
Errors in the quantum computation can originate from a variety of sources in the quantum hardware stack. Sycamore has 54-qubits and consists of over 140 individually tunable elements, each controlled with high-speed, analog electrical pulses. Achieving precise control over the whole device requires fine tuning more than 2,000 control parameters, and even small errors in these parameters can quickly add up to large errors in the total computation.
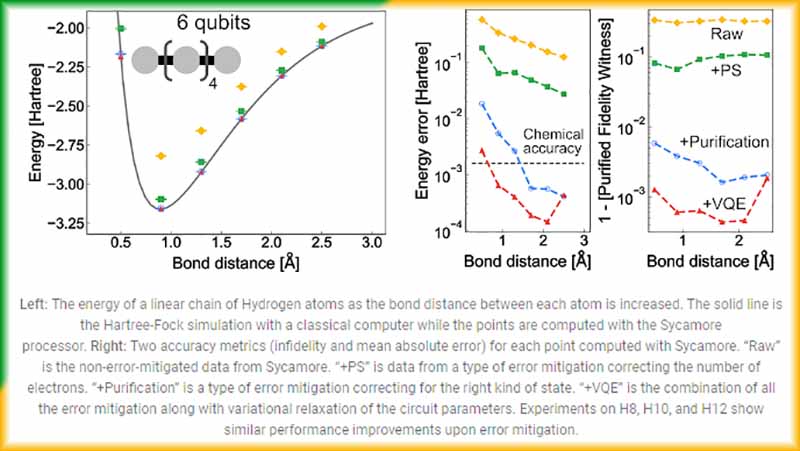
To accurately control the device, we use an automated framework that maps the control problem onto a graph with thousands of nodes, each of which represent a physics experiment to determine a single unknown parameter. Traversing this graph takes us from basic priors about the device to a high fidelity quantum processor, and can be done in less than a day. Ultimately, these techniques along with the algorithmic error mitigation enabled orders of magnitude reduction in the errors.
Pathways Forward
We hope that this experiment serves as a blueprint for how to run chemistry calculations on quantum processors, and as a jumping off point on the path to physical simulation advantage. One exciting prospect is that it is known how to modify the quantum circuits used in this experiment in a simple way such that they are no longer efficiently simulable, which would determine new directions for improved quantum algorithms and applications. We hope that the results from this experiment can be used to explore this regime by the broader research community. To run these experiments, you can find the code here.





